1/ 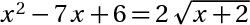 2/ 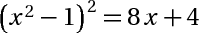 3/ 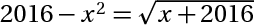 4/ 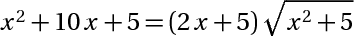 5/  6/  7/cho 3 số dương thõa mãn a +b +c+ ab +ac + bc = 6abc CM: 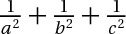 8/  9/cho x y z là ba số thực dương thõa mãn x+y+z = 1 . GTLN 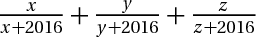 10/cho 2 số duong a,b thõa mãn 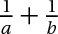 =2 GTLN 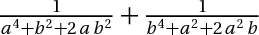 11/ x,y là số dương thõa mãn 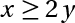 tìm GTNN 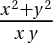 bài tuyển sinh vào lớp 10 khó quá nên em nhờ mấy men giải hộ Xem thêm: Mời mọi người tham gia cuộc thi do các Admin tổ chức CLICK! Cấu trúc đề thi cuộc thi VGT cấp THCS click!
1/ 2/3/4/5/6/7/cho 3 số dương thõa mãn a +b +c+ ab +ac + bc = 6abcCM: 8/9/cho x y z là ba số thực dương thõa mãn x+y+z = 1 . GTLN 10/cho 2 số duong a,b thõa mãn =2GTLN 11/ x,y là số dương thõa mãn tìm GTNN bài tuyển sinh vào lớp 10 khó quá nên em...
|
|
1,Cho số thực $x ,y$ thoả mãn $x\geq $y$\geq $1 Chứng minh bất đẳng thức: $\left ( 2016^{x} - 2016^{y} \right )\left ( \sqrt{1+x^{2}}+\sqrt{1+y^{2}} \right )$ $\geq$ $\left ( x-y \right )\left ( 2015\sqrt{1+x^{2}}-x+2015\sqrt{1+y^{2}}-y \right )$
2,Giải bất phương trình sau: $x^{3} - 4x^{2}+10x \geq \sqrt{3x-2}+6+4\sqrt{x-1}$
3,Trong mặt phẳng hệ trục toạ độ Oxy ,cho tam giác ABC vuông cân tại A. Gọi M là trung điểm cạnh AC, D điểm thuộc cạnh BC sao cho BD=2DC, H là hình chiếu vuông góc của D trên BM.Tìm toạ độ các đỉnh A,B,C biết D(-2,4), H$\left ( \frac{-18}{5} , \frac{24}{5} \right )$ và B có hoành độ nguyên.
1,Cho số thực $x ,y$ thoả mãn $x\geq $y$\geq $1 Chứng minh bất đẳng thức:$\left ( 2016^{x} - 2016^{y} \right )\left ( \sqrt{1+x^{2}}+\sqrt{1+y^{2}} \right )$ $\geq$ $\left ( x-y \right )\left ( 2015\sqrt{1+x^{2}}-x+2015\sqrt{1+y^{2}}-y \right )$...
|
|
Cho x và y là các số hữu tỉ thỏa mãn đẳng thức: $(x+y)^{3}=xy.(3x+3y+2)$. Chứng minh rằng: $\sqrt{1-xy}$ là một số hữu tỉ.
Chứng minh là số hữu tỉ
Cho x và y là các số hữu tỉ thỏa mãn đẳng thức: $(x+y)^{3}=xy.(3x+3y+2)$. Chứng minh rằng: $\sqrt{1-xy}$ là một số hữu tỉ.
|
|
|
|
|
Cho tam giác $ABC$ có trung tuyến $AM = \frac{AB}{2}$. Chứng minh: $sin^2 A = 2.sin^2 B + sin^2 C $
Giải nhanh nhá. Thanks
Cho tam giác $ABC$ có trung tuyến $AM = \frac{AB}{2}$. Chứng minh: $sin^2 A = 2.sin^2 B + sin^2 C $
|
|
1,Cho$f(x)=\sqrt{(m+1)x^{2} +2(m-1)x-3m+1}$ Tìm m để $f(x)$ xác định trên $[0;+\infty)$ 2, Tìm m để $f(x) :mx^{2}-2x+m+1 \geq 0 ,\forall x \geq 2$
1,Cho$f(x)=\sqrt{(m+1)x^{2} +2(m-1)x-3m+1}$Tìm m để $f(x)$ xác định trên $[0;+\infty)$2, Tìm m để $f(x) :mx^{2}-2x+m+1 \geq 0 ,\forall x \geq 2$
|
|
Giả sử $ a, b $ là các số nguyên dương sao cho $\frac{a+1}{b}+\frac{b+1}{a}$ là một số nguyên. Gọi $d$ là ước số chung của $a$ và $b$. Cmr $d\leq\sqrt{a+b}$
câu cuối đề học kỳ 2 toán 9 ninh bình 2010_2011
Giả sử $ a, b $ là các số nguyên dương sao cho $\frac{a+1}{b}+\frac{b+1}{a}$ là một số nguyên. Gọi $d$ là ước số chung của $a$ và $b$. Cmr $d\leq\sqrt{a+b}$
|
|
\begin{cases}x(y-3)-9y=1 \\ (x-1)^2y^2 +2y=-1 \end{cases}
Hệ phương trình 2 ẩn
\begin{cases}x(y-3)-9y=1 \\ (x-1)^2y^2 +2y=-1 \end{cases}
|
|
Gọi $x, y, z$ là khoảng cách từ điểm $M$ thuộc miền trong $\Delta ABC$ có 3 góc nhọn đến các cạnh $BC, CA, AB$. CMR: $\sqrt{x}+\sqrt{y}+\sqrt{z}\leq \sqrt{\frac{a^2+b^2+c^2}{2R}}$ $a, b, c$ là độ dài các cạnh của $\Delta$, $R$ là bán kính đường tròn ngoại tiếp. Dấu $"="$ xảy ra khi nào?
Gọi $x, y, z$ là khoảng cách từ điểm $M$ thuộc miền trong $\Delta ABC$ có 3 góc nhọn đến các cạnh $BC, CA, AB$. CMR:$\sqrt{x}+\sqrt{y}+\sqrt{z}\leq \sqrt{\frac{a^2+b^2+c^2}{2R}}$$a, b, c$ là độ dài các cạnh của $\Delta$, $R$ là bán kính đường tròn...
|
|
Tìm $n$, biết rằng : $n+S(n)=2014$ trong đó $S(n)$ là tổng các chữ số của $n$.
Tìm $n$, biết rằng :$n+S(n)=2014$ trong đó $S(n)$ là tổng các chữ số của $n$.
|
|
Tìm all các cặp STN $n$ và $k$ để $n^4+4^{2k+1}$ là số nguyên tố./
|
|
Cho (P) y=x2 và đường thẳng d:y=2mx-2m+1 .Tìm m để d cắt (P) tại 2 điểm A,B mà tiếp tuyến của (P) Tại A,B vuông góc với nhau
giúp mình với .....
Cho (P) y=x2 và đường thẳng d:y=2mx-2m+1 .Tìm m để d cắt (P) tại 2 điểm A,B mà tiếp tuyến của (P) Tại A,B vuông góc với nhau
|
|
giải phương trình $x^{2}+5x+4=(x-1+2\sqrt[3]{2x+3})(\sqrt{x+2}+1) \\ $
|
|
Cho các số thực không âm $a,b,c$ thỏa mãn $ab+bc+ca=1$. Chứng minh rằng: $\frac{1}{\sqrt{a+b}}+\frac{1}{\sqrt{b+c}}+\frac{1}{\sqrt{c+a}}\geq \sqrt{2}+\sqrt{\frac{1}{2}}$
Cho các số thực không âm $a,b,c$ thỏa mãn $ab+bc+ca=1$. Chứng minh rằng: $\frac{1}{\sqrt{a+b}}+\frac{1}{\sqrt{b+c}}+\frac{1}{\sqrt{c+a}}\geq \sqrt{2}+\sqrt{\frac{1}{2}}$
|
|
Tìm a,b để hệ sau có nghiệm duy nhất [chuyên toán ninh bình 2001-2002] $\left\{ \begin{array}{l} xyz + z =a\\ xyz^{2} +z=b\\ x^{2}+y^{2}+z^{2}=4\end{array} \right.$
Hệ phương trình chứa tham số
Tìm a,b để hệ sau có nghiệm duy nhất [chuyên toán ninh bình 2001-2002]$\left\{ \begin{array}{l} xyz + z =a\\ xyz^{2} +z=b\\ x^{2}+y^{2}+z^{2}=4\end{array} \right.$
|
|
cho $a, b, c\in R^{+}$ và thỏa mãn $ab+bc+ca=1$ .chứng minh rằng:$(1+a)(1-b)(1-c)(\frac{a}{1-a^{2}}+\frac{b}{1-b^{2}}+\frac{c}{1-c^{2}})=\frac{4abc}{(1-a)(1+b)(1+c)}$
với $a, b, c\neq 1$ nha....!?
cơ mà làm theo cách nào đơn giản mà dễ hiểu nhất...!?
cho $a, b, c\in R^{+}$ và thỏa mãn $ab+bc+ca=1$ .chứng minh rằng:$(1+a)(1-b)(1-c)(\frac{a}{1-a^{2}}+\frac{b}{1-b^{2}}+\frac{c}{1-c^{2}})=\frac{4abc}{(1-a)(1+b)(1+c)}$với $a, b, c\neq 1$ nha....!?
|
|
Tìm số thực m lớn nhất sao cho tồn tại các số thực không âm x,y,z thỏa mãn:\begin{cases}x+y+z=4 \\ x^3+y^3+z^3+8(xy^2+yz^2+zx^2)=m \end{cases}
|
|
Bài 3 : Chứng minh các bất đẳng thức : - Cho a + b + c = 0 . Chứng minh rằng : a3 + b3 + c3 = 3abc.
- Cho a, b, c là độ dài ba cạnh của tam giác. Chứng minh rằng :

- Chứng minh rằng : x5 + y5 ≥ x4y + xy4 với x, y ≠ 0 và x + y ≥ 0
Bài 4 : giải phương trình : - x2 – 3x + 2 + |x – 1| = 0
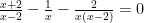
Bài 5 : tìm giá trị lớn nhất và nhỏ nhất (nếu có) - A = x2 – 2x + 5
- B = -2x2 – 4x + 1.
- C =

Bài 6 : tính giá trị của biểu thức. - Biết a – b = 7 tính : A = a2(a + 1) – b2(b – 1) + ab – 3ab(a – b + 1)
- Cho ba số a, b, c khác 0 thỏa nãm đẳng thức :

Tính : P = 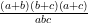
mọi người ơi !!!!!!!!!
Bài 3 : Chứng minh các bất đẳng thức :Cho a + b + c = 0 . Chứng minh rằng : a3 + b3 + c3 = 3abc.Cho a, b, c là độ dài ba cạnh của tam giác. Chứng minh rằng :Chứng minh rằng : x5 + y5 ≥ x4y + xy4 với x, y ≠ 0 và x + y ≥ 0Bài 4 : giải phương trình :x2...
|
|
CMR: $A=1^n+2^n+3^n+....+x^n$ chia hết cho $B=1+2+3+...+x$ với $x;n$ và là các số nguyên dương và $n$ lẻ
|
|
Cho $\sqrt{x^{2}+\sqrt[3]{x^{4}y^{2}}} +\sqrt{y^{2}+\sqrt[3]{x^{2}y^{4}}}$=a. Chứng minh: $\sqrt[3]{x^{2}}+\sqrt[3]{y^{2}}=\sqrt[3]{a^{2}}$
Cho $\sqrt{x^{2}+\sqrt[3]{x^{4}y^{2}}} +\sqrt{y^{2}+\sqrt[3]{x^{2}y^{4}}}$=a.Chứng minh: $\sqrt[3]{x^{2}}+\sqrt[3]{y^{2}}=\sqrt[3]{a^{2}}$
|
|
Cho khai triển:$(1+x+x^2)^{2016}=a_{o}+a_{1}x+a_{2}x^2+...+a_{4032}.x^{4032}$.
Tính giá trị biểu thức: $H=C^{0}_{2016}.a_{3} -C^{1}_{2016}.a_{2}+C^{2}_{2016}.a_{1}-C^{3}_{2016}.a_{0}$
Cho khai triển:$(1+x+x^2)^{2016}=a_{o}+a_{1}x+a_{2}x^2+...+a_{4032}.x^{4032}$. Tính giá trị biểu thức: $H=C^{0}_{2016}.a_{3} -C^{1}_{2016}.a_{2}+C^{2}_{2016}.a_{1}-C^{3}_{2016}.a_{0}$
|
|
Có một cái ao bên trong chứa mạch nước ngầm. Để tát cạn nước ở trong ao, nta dùng $7$ chiếc máy bơm thì hết $5$ phút còn nếu dùng $4$ chiếc máy bơm thì hết $10$ phút. Hỏi : Để tát cạn nước ao trong $6$ phút , nta cần dùng bn chiếc máy bơm ?
Bài toán Niutơn
Có một cái ao bên trong chứa mạch nước ngầm. Để tát cạn nước ở trong ao, nta dùng $7$ chiếc máy bơm thì hết $5$ phút còn nếu dùng $4$ chiếc máy bơm thì hết $10$ phút. Hỏi : Để tát cạn nước ao trong $6$ phút , nta cần dùng bn chiếc máy bơm ?
|
|
TÍNH A \begin{cases}A=\frac{4.1}{4.1^{4}+1}+\frac{4.2}{4.2^{4}+1}+\frac{4.3}{4.3^{4}+1}+...+\frac{4.n}{4.n^{4}+1}\\ \end{cases}
luyện tập ik nào mấy chế
TÍNH A \begin{cases}A=\frac{4.1}{4.1^{4}+1}+\frac{4.2}{4.2^{4}+1}+\frac{4.3}{4.3^{4}+1}+...+\frac{4.n}{4.n^{4}+1}\\ \end{cases}
|
|
$1.\mathop {\lim }\limits_{x \to 0}\frac{\cos 2x-1}{sin^{2}3x}$ $2.\mathop {\lim }\limits_{x \to 0}\frac{\tan x-\sin x}{x^{3}}$
$1.\mathop {\lim }\limits_{x \to 0}\frac{\cos 2x-1}{sin^{2}3x}$$2.\mathop {\lim }\limits_{x \to 0}\frac{\tan x-\sin x}{x^{3}}$
|
|
tìm số tiếp và nêu quy luật 14, 16, 28, 32, 42, 48, 56, 64, ?,
nữa nhé !!!!!!!!!
tìm số tiếp và nêu quy luật14, 16, 28, 32, 42, 48, 56, 64, ?,
|
|
cho a,b,c là các số thực dương. chứng minh rằng:$\frac{2a}{b+c}+\frac{2b}{c+a}+\frac{2c}{a+b}\geq 3+\frac{(a-b)^2+(b-c)^2+(c-a)^2}{(a+b+c)^2}$
|
|
Cho x,y,z>0 thỏa mãn: $xyz\geq 1; z\leq 1$. Tìm GTNN:$P=\frac{x}{1+y}+\frac{y}{1+x}+\frac{4-z^3}{3+3xy}$
|
|
Cho tam giác ABC thỏa mãn $\frac{a^2+b^2}{m_{c}}+\frac{b^2+c^2}{m_{a}}+\frac{c^2+b^2}{m_{b}}=12R$. CM: tam giác ABC đều
Mọi người giúp mình bài này với
Cho tam giác ABC thỏa mãn $\frac{a^2+b^2}{m_{c}}+\frac{b^2+c^2}{m_{a}}+\frac{c^2+b^2}{m_{b}}=12R$. CM: tam giác ABC đều
|
|
cho các số thực$ x,y,z$ thỏa mãn:\begin{cases}x-y+z=3 \\ x^2+y^2+z^2=5 \end{cases}.Tìm giá trị nhỏ nhất của:$P=\frac{x+y-2}{z+2}$
|
|
$\sqrt{2x+1+\sqrt{x+1} } +\sqrt{2x-\sqrt{x+1}} = 2\sqrt{x+1} +1$ $\sqrt{x^{2} -8x +15} + \sqrt{x^{2}+2x-15} \leq \sqrt{4x^{2}-18x+18}$
$\sqrt{2x+1+\sqrt{x+1} } +\sqrt{2x-\sqrt{x+1}} = 2\sqrt{x+1} +1$$\sqrt{x^{2} -8x +15} + \sqrt{x^{2}+2x-15} \leq \sqrt{4x^{2}-18x+18}$
|
|
Chứng minh rằng với mọi số tự nhiên $n \neq 0$ ta đều có :$\frac{1}{2.5}+\frac{1}{5.8}+\frac{1}{8.11}+...+\frac{1}{(3n-1).(3n+2)}=\frac{n}{6n+4}$
|
|
trong mp 0xy cho tam giác
ABC vuông cân tại A , gọi M là trung điểm BC , G là trọng tâm ABM D ( 7;2) là
điểm năm trên đoạn MC sao cho GA=GD =>> viết PT đt AB biêt A có x <4
va pt đt GA 3x-y-13 = 0
bài của vesaucaumay nè
trong mp 0xy cho tam giác
ABC vuông cân tại A , gọi M là trung điểm BC , G là trọng tâm ABM D ( 7;2) là
điểm năm trên đoạn MC sao cho GA=GD =>> viết PT đt AB biêt A có x <4
va pt đt GA 3x-y-13 = 0
|
|
cho tam giác $ABC$ có các góc, cạnh thỏa mãn hệ thức$\begin{cases}cotA+cotC=cotB \\ b(b^2-a^2)+c(c^2-a^2)=0 \end{cases}$tìm các góc cảu tam giác $ABC$
|
|
cho $ a,b,c $ là độ dài ba cạnh của một tam giác không nhọn. CMR$(a^2+b^2+c^2)(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2})\geq 10$
|
|
cho các số dương $ab+bc+ca=3$<div>chứng minh rằng $\frac{1}{1+a^2(b+c)}+\frac{1}{1+b^2(c+a)}+\frac{1}{1+c^2(a+b)}\leq \frac{1}{abc}$
|
|
\begin{cases}\sqrt{x^{2}+2y+3}+2y-3=0 \\ 2(2y^3+x^3)+3y(x+1)^2+6x(x+1)+2=0 \end{cases}
EXO CHANYEOL
\begin{cases}\sqrt{x^{2}+2y+3}+2y-3=0 \\ 2(2y^3+x^3)+3y(x+1)^2+6x(x+1)+2=0 \end{cases}
|
|
$\begin{cases}5x^{2}y-4xy^{2}+3y^3-2(x+y)=0 \\ yx(x^{2}+y^{2})+2=(x+y)^2 \end{cases}$
exo SEHUN
$\begin{cases}5x^{2}y-4xy^{2}+3y^3-2(x+y)=0 \\ yx(x^{2}+y^{2})+2=(x+y)^2 \end{cases}$
|
|
\begin{cases}(x-1)(y^{2}+6)=y(x^{2}+1) \\ (y-1)(x^{2}+6)=x(y^{2}+1) \end{cases}
làm jup vs
\begin{cases}(x-1)(y^{2}+6)=y(x^{2}+1) \\ (y-1)(x^{2}+6)=x(y^{2}+1) \end{cases}
|
|
\begin{cases}\sqrt{x+1}+y=\sqrt{y+1}+x \\ x^{2}+2xy-y^{2}=4 \end{cases}
lm chi tiết jum nhé
\begin{cases}\sqrt{x+1}+y=\sqrt{y+1}+x \\ x^{2}+2xy-y^{2}=4 \end{cases}
|
|
$\frac{(x^{3}+3x^{2}\sqrt{x+1})(3-x)}{2+\sqrt{x+1}}\leq 4(x+1)(2\sqrt{x+1}-x-1)$
giải bpt
$\frac{(x^{3}+3x^{2}\sqrt{x+1})(3-x)}{2+\sqrt{x+1}}\leq 4(x+1)(2\sqrt{x+1}-x-1)$
|
|
$3\sqrt{2(3x+4)^{3}}\leq (x^{2}+2x-2)\sqrt{x^{2}+2x-3}+(19x+26).\sqrt{x+1}$
Làm nhanh+ Vote nhiều
$3\sqrt{2(3x+4)^{3}}\leq (x^{2}+2x-2)\sqrt{x^{2}+2x-3}+(19x+26).\sqrt{x+1}$
|
|
cho 5 số thực dương thỏa mãn a+b+c+d+e=5. tìm GTNN của biểu thức
$P=(\frac{a}{a+2})^{3}+(\frac{b}{b+2})^{3}+(\frac{c}{c+2})^{3}+(\frac{d}{d+2})^{3}+(\frac{e}{e+2})^{3}$
cho 5 số thực dương thỏa mãn a+b+c+d+e=5. tìm GTNN của biểu thức$P=(\frac{a}{a+2})^{3}+(\frac{b}{b+2})^{3}+(\frac{c}{c+2})^{3}+(\frac{d}{d+2})^{3}+(\frac{e}{e+2})^{3}$
|
|
cho 2 số dương $x$ va $y$ biết $x+y=1$ .Tìm GTNN của $B=(1-1/x^{2})(1-1/y^{2})$
|
|
Tìm Max:$\sqrt{x-2}+\sqrt{4-x}+6\sqrt{x+6}-x^2+5x+1992$
Tìm Max:$\sqrt{x-2}+\sqrt{4-x}+6\sqrt{x+6}-x^2+5x+1992$
|
|
$\frac{2x^{4}+2x^{2}}{\sqrt{x+1}} +(x+2)\sqrt{x+1}\geq x^{3} +2x^{2}+5x$
giải bpt
$\frac{2x^{4}+2x^{2}}{\sqrt{x+1}} +(x+2)\sqrt{x+1}\geq x^{3} +2x^{2}+5x$
|
|
Cho 3 số thực $x,y,z \in \left[ {1;4} \right]$ và thỏa mãn $x+y+z=6$ . Tìm Min : $T=\frac{z}{8(x^{2}+y^{2})}+\frac{x^{2}+y^{2}-1}{xyz}$
|
|
cho $a,b,c>0$ thỏa mãn $2006ac+ab+bc=2006$ . Tìm $Max$: P=$\frac{2}{a^{2}+1} -\frac{2b^{2}}{b^{2}+2006^{2}} +\frac{3}{c^{2}+1}$
cho $a,b,c>0$ thỏa mãn $2006ac+ab+bc=2006$ . Tìm $Max$: P=$\frac{2}{a^{2}+1} -\frac{2b^{2}}{b^{2}+2006^{2}} +\frac{3}{c^{2}+1}$
|
|
$6x\sqrt{x^{2}-1}-\sqrt{x^{2}+8x}=6x^{2}-x-8$
|
|
$3x(2+\sqrt{9x^{2}+3})+(4x+2)(1+\sqrt{x^{2}+x+1})=0$
Làm nhanh hộ nha
$3x(2+\sqrt{9x^{2}+3})+(4x+2)(1+\sqrt{x^{2}+x+1})=0$
|
|
Bài 1. $\begin{cases}\sqrt{2x-y-1}+\sqrt{3y+1}=\sqrt{x}+\sqrt{x+2y} \\ x^{3}-3x+2= 2y^{3}-y^{2}\end{cases}$Bài 2. $3(x^{2}-2) + \frac{4\sqrt{2}}{\sqrt{x^{2}-x+1}} > \sqrt{x}(\sqrt{x-1} + 3\sqrt{x^{2}-1})$
|