cho $a, b, c\in R^{+}$ và thỏa mãn $ab+bc+ca=1$ .chứng minh rằng:$(1+a)(1-b)(1-c)(\frac{a}{1-a^{2}}+\frac{b}{1-b^{2}}+\frac{c}{1-c^{2}})=\frac{4abc}{(1-a)(1+b)(1+c)}$
với $a, b, c\neq 1$ nha....!?
cơ mà làm theo cách nào đơn giản mà dễ hiểu nhất...!?
cho $a, b, c\in R^{+}$ và thỏa mãn $ab+bc+ca=1$ .chứng minh rằng:$(1+a)(1-b)(1-c)(\frac{a}{1-a^{2}}+\frac{b}{1-b^{2}}+\frac{c}{1-c^{2}})=\frac{4abc}{(1-a)(1+b)(1+c)}$với $a, b, c\neq 1$ nha....!?
|
|
Tìm số thực m lớn nhất sao cho tồn tại các số thực không âm x,y,z thỏa mãn:\begin{cases}x+y+z=4 \\ x^3+y^3+z^3+8(xy^2+yz^2+zx^2)=m \end{cases}
|
|
Bài 3 : Chứng minh các bất đẳng thức : - Cho a + b + c = 0 . Chứng minh rằng : a3 + b3 + c3 = 3abc.
- Cho a, b, c là độ dài ba cạnh của tam giác. Chứng minh rằng :

- Chứng minh rằng : x5 + y5 ≥ x4y + xy4 với x, y ≠ 0 và x + y ≥ 0
Bài 4 : giải phương trình : - x2 – 3x + 2 + |x – 1| = 0
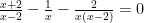
Bài 5 : tìm giá trị lớn nhất và nhỏ nhất (nếu có) - A = x2 – 2x + 5
- B = -2x2 – 4x + 1.
- C =

Bài 6 : tính giá trị của biểu thức. - Biết a – b = 7 tính : A = a2(a + 1) – b2(b – 1) + ab – 3ab(a – b + 1)
- Cho ba số a, b, c khác 0 thỏa nãm đẳng thức :

Tính : P = 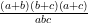
mọi người ơi !!!!!!!!!
Bài 3 : Chứng minh các bất đẳng thức :Cho a + b + c = 0 . Chứng minh rằng : a3 + b3 + c3 = 3abc.Cho a, b, c là độ dài ba cạnh của tam giác. Chứng minh rằng :Chứng minh rằng : x5 + y5 ≥ x4y + xy4 với x, y ≠ 0 và x + y ≥ 0Bài 4 : giải phương trình :x2...
|
|
CMR: $A=1^n+2^n+3^n+....+x^n$ chia hết cho $B=1+2+3+...+x$ với $x;n$ và là các số nguyên dương và $n$ lẻ
|
|
Cho $\sqrt{x^{2}+\sqrt[3]{x^{4}y^{2}}} +\sqrt{y^{2}+\sqrt[3]{x^{2}y^{4}}}$=a. Chứng minh: $\sqrt[3]{x^{2}}+\sqrt[3]{y^{2}}=\sqrt[3]{a^{2}}$
Cho $\sqrt{x^{2}+\sqrt[3]{x^{4}y^{2}}} +\sqrt{y^{2}+\sqrt[3]{x^{2}y^{4}}}$=a.Chứng minh: $\sqrt[3]{x^{2}}+\sqrt[3]{y^{2}}=\sqrt[3]{a^{2}}$
|
|
Cho khai triển:$(1+x+x^2)^{2016}=a_{o}+a_{1}x+a_{2}x^2+...+a_{4032}.x^{4032}$.
Tính giá trị biểu thức: $H=C^{0}_{2016}.a_{3} -C^{1}_{2016}.a_{2}+C^{2}_{2016}.a_{1}-C^{3}_{2016}.a_{0}$
Cho khai triển:$(1+x+x^2)^{2016}=a_{o}+a_{1}x+a_{2}x^2+...+a_{4032}.x^{4032}$. Tính giá trị biểu thức: $H=C^{0}_{2016}.a_{3} -C^{1}_{2016}.a_{2}+C^{2}_{2016}.a_{1}-C^{3}_{2016}.a_{0}$
|
|
Có một cái ao bên trong chứa mạch nước ngầm. Để tát cạn nước ở trong ao, nta dùng $7$ chiếc máy bơm thì hết $5$ phút còn nếu dùng $4$ chiếc máy bơm thì hết $10$ phút. Hỏi : Để tát cạn nước ao trong $6$ phút , nta cần dùng bn chiếc máy bơm ?
Bài toán Niutơn
Có một cái ao bên trong chứa mạch nước ngầm. Để tát cạn nước ở trong ao, nta dùng $7$ chiếc máy bơm thì hết $5$ phút còn nếu dùng $4$ chiếc máy bơm thì hết $10$ phút. Hỏi : Để tát cạn nước ao trong $6$ phút , nta cần dùng bn chiếc máy bơm ?
|
|
TÍNH A \begin{cases}A=\frac{4.1}{4.1^{4}+1}+\frac{4.2}{4.2^{4}+1}+\frac{4.3}{4.3^{4}+1}+...+\frac{4.n}{4.n^{4}+1}\\ \end{cases}
luyện tập ik nào mấy chế
TÍNH A \begin{cases}A=\frac{4.1}{4.1^{4}+1}+\frac{4.2}{4.2^{4}+1}+\frac{4.3}{4.3^{4}+1}+...+\frac{4.n}{4.n^{4}+1}\\ \end{cases}
|
|
$1.\mathop {\lim }\limits_{x \to 0}\frac{\cos 2x-1}{sin^{2}3x}$ $2.\mathop {\lim }\limits_{x \to 0}\frac{\tan x-\sin x}{x^{3}}$
$1.\mathop {\lim }\limits_{x \to 0}\frac{\cos 2x-1}{sin^{2}3x}$$2.\mathop {\lim }\limits_{x \to 0}\frac{\tan x-\sin x}{x^{3}}$
|
|
tìm số tiếp và nêu quy luật 14, 16, 28, 32, 42, 48, 56, 64, ?,
nữa nhé !!!!!!!!!
tìm số tiếp và nêu quy luật14, 16, 28, 32, 42, 48, 56, 64, ?,
|
|
cho a,b,c là các số thực dương. chứng minh rằng:$\frac{2a}{b+c}+\frac{2b}{c+a}+\frac{2c}{a+b}\geq 3+\frac{(a-b)^2+(b-c)^2+(c-a)^2}{(a+b+c)^2}$
|
|
Cho x,y,z>0 thỏa mãn: $xyz\geq 1; z\leq 1$. Tìm GTNN:$P=\frac{x}{1+y}+\frac{y}{1+x}+\frac{4-z^3}{3+3xy}$
|
|
Cho tam giác ABC thỏa mãn $\frac{a^2+b^2}{m_{c}}+\frac{b^2+c^2}{m_{a}}+\frac{c^2+b^2}{m_{b}}=12R$. CM: tam giác ABC đều
Mọi người giúp mình bài này với
Cho tam giác ABC thỏa mãn $\frac{a^2+b^2}{m_{c}}+\frac{b^2+c^2}{m_{a}}+\frac{c^2+b^2}{m_{b}}=12R$. CM: tam giác ABC đều
|
|
cho các số thực$ x,y,z$ thỏa mãn:\begin{cases}x-y+z=3 \\ x^2+y^2+z^2=5 \end{cases}.Tìm giá trị nhỏ nhất của:$P=\frac{x+y-2}{z+2}$
|
|
$\sqrt{2x+1+\sqrt{x+1} } +\sqrt{2x-\sqrt{x+1}} = 2\sqrt{x+1} +1$ $\sqrt{x^{2} -8x +15} + \sqrt{x^{2}+2x-15} \leq \sqrt{4x^{2}-18x+18}$
$\sqrt{2x+1+\sqrt{x+1} } +\sqrt{2x-\sqrt{x+1}} = 2\sqrt{x+1} +1$$\sqrt{x^{2} -8x +15} + \sqrt{x^{2}+2x-15} \leq \sqrt{4x^{2}-18x+18}$
|